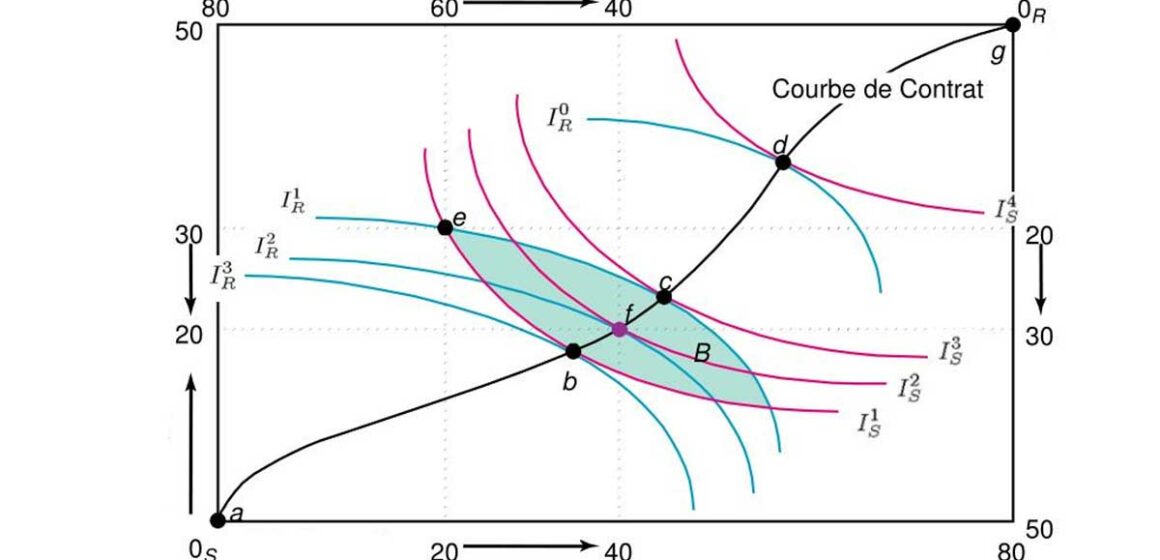
La boîte d’Edgeworth, du nom de son inventeur, Francis Ysidro Edgeworth (1845-1926), est un moyen graphique de représenter la distribution potentielle des ressources en prenant les courbes d’indifférence de deux individus. Edgeworth a apporté d’importantes contributions à la théorie économique néoclassique et au développement des statistiques économiques. Il a présenté ce sujet ainsi que les courbes d’indifférence dans son livre Mathematical Psychis : An Essay on the Application of Mathematics to the Moral Sciences en 1881.


Bien qu’il ait été accueilli avec indifférence à l’époque, il a été loué par Irving Fisher dans sa thèse de doctorat et a eu une énorme influence sur Alfred Marshall, qui l’a exprimé dans ses Principes d’économie de 1890. Son travail a été développé par Wilfredo Pareto en 1906 et popularisé par l’exposé d’Arthur Bowley. La version moderne de la figure est communément appelée la boîte d’Edgeworth-Bowley. Ce concept d’économie est consacré à la boîte d’Edgeworth et à ses propositions sur la distribution des ressources.
La boîte d’Edgeworth est un outil graphique analytique souvent utilisé dans la théorie de l’équilibre général, qui peut aider à trouver l’équilibre concurrentiel d’un système simple. Elle permet de représenter les dotations et les préférences de deux personnes et d’analyser le processus d’échange. Pour cela, il faut se souvenir des courbes d’indifférence individuelles et du fait qu’elles ne disaient rien sur la quantité de ressources. Cette fois, les ressources sont fixes (potentielles) et l’interaction se fait entre deux personnes (dans ce cas, Alex et Benjamin) qui doivent se partager une quantité fixe de biens 1 et 2.
La boîte d’Edgeworth est un diagramme rectangulaire dans lequel Alex et Benjamin (A et B) sont placés sur les bords tandis que la mesure des biens est effectuée sur les axes. Le bien 1 est mesuré horizontalement et le bien 2 verticalement. On constate que les diagrammes de A et B sont identiques, mais que l’un d’entre eux a été inversé pour recouvrir l’autre et former la boîte. La largeur de la boîte est la quantité totale du bien 1 et sa hauteur est la quantité totale du bien 2. Par conséquent, chaque répartition possible des biens entre les deux personnes peut être représentée par un point à l’intérieur de la boîte. Une allocation de ressources est dite réalisable si la quantité totale utilisée de chaque bien est égale à la quantité totale disponible. Cela signifie que
quantité totale du bien 1 = quantité du bien 1 de A + quantité du bien 1 de B.
Il en va de même pour le bien 2.
Dans cette analyse, des courbes d’indifférence sont tracées pour A et B représentant les combinaisons de biens 1 et 2 qui satisfont le même niveau d’utilité. Rappelons que le long de la courbe d’indifférence, l’utilité ou la satisfaction reste constante, quelle que soit la valeur monétaire. Et à mesure que l’on s’éloigne de l’origine, le niveau d’utilité augmente. Ceci indique que la courbe a2 a une utilité supérieure à la courbe a1, que la courbe a3 a une utilité supérieure à la courbe a2, etc, idem pour les courbes d’indifférence de l’individu B.
Un point qui mérite un intérêt particulier est l’allocation correspondant à la dotation initiale de A et B, qui est l’allocation à partir de laquelle les consommateurs démarrent et qui est indiquée dans le graphique par la lettre W. Comme nous pouvons le voir, dans cette dotation initiale, toutes les ressources du bien 1 et du bien 2 sont épuisées : A se situe sur la courbe a3 et B sur sa courbe b2 ; chacun consommant les quantités potentielles des biens 1 et 2.
Examinons les courbes d’indifférence passant par la dotation initiale W, a3 et b2. La zone dans laquelle A jouit d’un bien-être supérieur à la dotation initiale est formée par tous les paniers passant par W (au-dessus et à droite). À son tour, la zone dans laquelle B jouit d’un bien-être supérieur est formée par toutes les allocations situées au-dessus (de son point de vue) de sa courbe d’indifférence passant par W (de notre point de vue, en bas, à gauche). Notez la zone aplatie formée par les courbes d’indifférence a3 et b2, colorées en orange dans le graphique. Tout point situé dans cette zone est mutuellement avantageux pour A et B. Cependant, le processus de négociation qui doit être mené pour atteindre un niveau d’utilité plus élevé implique l’abandon d’une partie du bien détenu en excès.
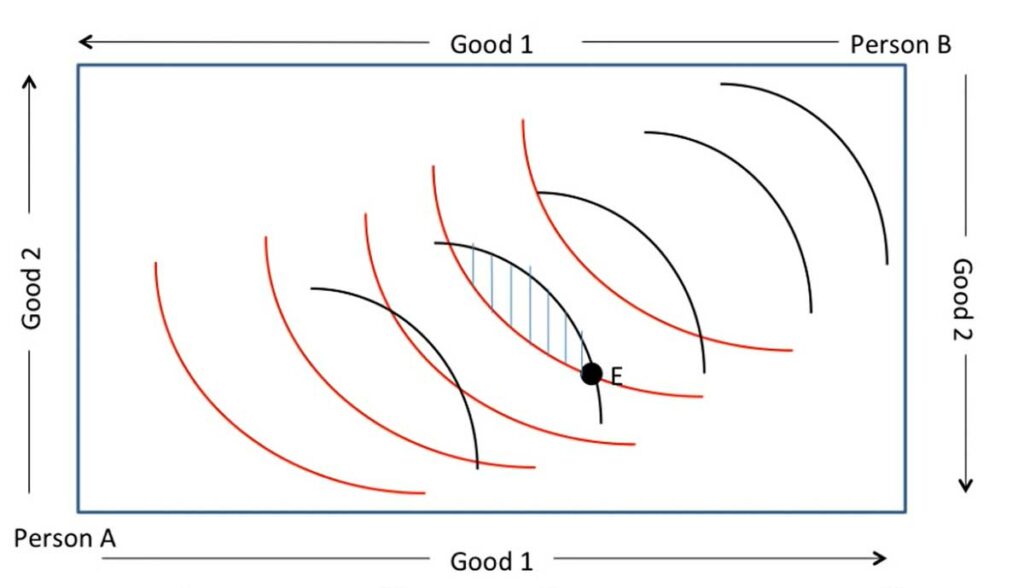
Comme nous l’avons évoqué dans d’autres articles, les contributions morales de l’économie classique ont toujours été au centre de l’analyse. Dans ce cas, la région rétrécie est une zone qui offre des avantages mutuels et un niveau potentiel d’échanges, mais pour accéder à une partie du bien plus rare, il faut renoncer à une partie du bien que l’on possède en plus grande abondance. L’idée que les ressources sont limitées est à l’origine de la pensée économique, d’où la nécessité de rechercher une efficacité maximale dans leur utilisation. Cette efficacité permet d’améliorer l’équité et la dotation initiale.
La boîte d’Edgeworth illustre plusieurs concepts clés des mécanismes d’échange et des actions qui contribuent au processus d’allocation efficace et d’amélioration de l’équité. Chaque point de tangence entre les courbes d’indifférence de A et B (tels que les points E et F sur le graphique), sont des points d’allocations efficaces au sens de Pareto. Une allocation est dite efficace au sens de Pareto lorsqu’il n’est pas possible d’améliorer le bien-être de l’un des agents sans détériorer celui de l’autre, c’est-à-dire lorsqu’aucun échange mutuellement avantageux n’est possible.
En ce sens, l’importance de la dotation initiale est essentielle pour comprendre le niveau d’efficacité qu’il est possible d’atteindre par un simple échange. Il convient de noter que ces points efficaces, au sens de Pareto, rejoignent les deux bords de la boîte sur cette ligne imaginaire connue sous le nom de courbe de contrat (couleur verte dans le graphique). Ce terme repose sur l’idée que tous les contrats d’échange définitifs doivent se situer dans l’ensemble de Pareto, sinon ils ne seraient pas définitifs puisque le bien-être des deux parties pourrait encore être amélioré.